Category:Eigenfunction Matching Method

Introduction

A method for solving wave scattering problems in which the solution can be solve in various regions using separation of variables. The solution in these regions are then matched at various boundaries. The simplest problem is in Wavemaker Theory, but the separation of variables is also described in Dispersion Relation for a Free Surface

The method is described in Linton and McIver 2001. All that is required is that the domain consists of water of constant depth and that there are suitable conditions that we can separate variables. For each problem considered, the simplest case is the semi-infinite domain on one side and open water on the other, and it is this problem that we focus on in particular. The problem can then be extended to a finite domain, using Symmetry in Two Dimensions and the problem can also be extended to circular regions in three-dimensions.

The method is also called the mode matching method.

Typical Problems

There is no end to the problems which an be solved by this method, and we try to present here the solutions for some of the typical problems. As stated previously, we begin with the semi-infinite problem with open water on the left and waves incident from the left and extend this problem to the finite depth problem by Symmetry in Two Dimensions and to the circular problem.

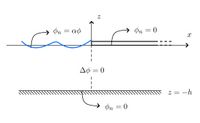
Dock

Wave scattering by a semi-infinite dock

The semi-infinite problem is shown on the right.

We have the following solutions for this case.

• Eigenfunction Matching for a Semi-Infinite Dock
• Eigenfunction Matching for a Finite Dock
• Eigenfunction Matching for a Finite Dock using Symmetry
• Two Identical Docks using Symmetry
• Eigenfunction Matching for a Circular Dock

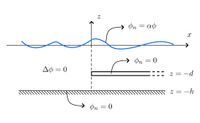
Submerged Dock

Wave scattering by a submerged semi-infinite dock

The submerged semi-infinite problem is shown on the right.

We have the following solutions for this case.

• Eigenfunction Matching for a Submerged Semi-Infinite Dock
• Eigenfunction Matching for a Submerged Finite Dock
• Two Identical Submerged Docks using Symmetry
• Eigenfunction Matching for a Submerged Circular Dock

Floating Elastic Plate

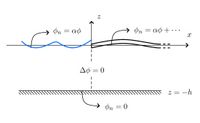
Wave scattering by a submerged semi-infinite elastic plate

The submerged semi-infinite problem is shown on the right.

We have the following solutions for this case.

• Eigenfunction Matching for a Semi-Infinite Floating Elastic Plate
• Eigenfunction Matching for a Finite Floating Elastic Plate using Symmetry
• Eigenfunction Matching Method for Floating Elastic Plates
• Eigenfunction Matching for a Circular Floating Elastic Plate

Submerged Rectangle

• Eigenfunction Matching for a Semi-Infinite Rectangle

Change in Depth

• Eigenfunction Matching for a Semi-Infinite Change in Depth
• Eigenfunction Matching for a Finite Change in Depth

Vertical Fixed Plate

• Eigenfunction Matching for a Vertical Fixed Plate