Linear Theory of Ocean Surface Waves
Introduction
Looking out to sea from the shore, we can see waves on the sea surface. Looking carefully, we notice the waves are undulations of the sea surface with a height of around a meter, where height is the vertical distance between the bottom of a trough and the top of a nearby crest. The wavelength, which we might take to be the distance between prominent crests, is around 50m - 100m. Watching the waves for a few minutes, we notice that wave-height and wave-length are not constant. The heights vary randomly in time and space, and the statistical properties of the waves, such as the mean height averaged for a few hundred waves, change from day to day. These prominent offshore waves are generated by wind. Sometimes the local wind generates the waves, other times distant storms generate waves which ultimately reach the coast. For example, waves breaking on the Southern California coast on a summer day may come from vast storms offshore of Antarctica 10,000km away.
If we watch closely for a long time, we notice that sea level changes from hour to hour. Over a period of a day, sea level increases and decreases relative to a point on the shore by about a meter. The slow rise and fall of sea level is due to the tides, another type of wave on the sea surface. Tides have wavelengths of thousands of kilometers, and they are generated by the slow, very small changes in gravity due to the motion of the sun and the moon relative to Earth.
Surface waves are inherently nonlinear: The solution of the equations of motion depends on the surface boundary conditions, but the surface boundary conditions are the waves we wish to calculate. How can we proceed?
We begin by assuming that the amplitude of waves on the water surface is infinitely small so the surface is almost exactly a plane. To simplify the mathematics, we can also assume that the flow is 2-dimensional with waves traveling in the x-direction. We also assume that the Coriolis force and viscosity can be neglected. If we retain rotation, we get Kelvin waves.
With these assumptions, the sea-surface elevation [math]\displaystyle{ \zeta\ }[/math] of a wave traveling in the [math]\displaystyle{ x }[/math] direction is:
[math]\displaystyle{ \zeta\ = a \sin(kx - \omega t) \,\! }[/math]
with
[math]\displaystyle{ \omega = 2 \pi\,f = \frac{2\pi}{T}; \qquad k = \frac{2\pi}{\lambda} \,\! }[/math]
where [math]\displaystyle{ \omega }[/math] is wave frequency in radians per second, [math]\displaystyle{ f }[/math] is the wave frequency in Hertz (Hz), [math]\displaystyle{ k }[/math] is wave number, [math]\displaystyle{ T }[/math] is wave period, [math]\displaystyle{ \lambda }[/math] is wave-length, and where we assume, as stated above, that [math]\displaystyle{ k a = O (0) }[/math].
The wave period [math]\displaystyle{ T }[/math] is the time it takes two successive wave crests or troughs to pass a fixed point. The wave-length [math]\displaystyle{ \lambda }[/math] is the distance between two successive wave crests or troughs at a fixed time.
Dispersion Relation
Wave frequency [math]\displaystyle{ \omega }[/math] is related to wave number [math]\displaystyle{ k }[/math] by the dispersion relation (Lamb 1932 §228):
[math]\displaystyle{ \omega^2 = gk\tanh(kh) \,\! }[/math]
where [math]\displaystyle{ h }[/math] is the water depth and [math]\displaystyle{ g }[/math] is the acceleration of gravity.
Two approximations are especially useful.
- Deep-water approximation is valid if the water depth [math]\displaystyle{ h }[/math] is much greater than the wave-length [math]\displaystyle{ L }[/math]. In this case, [math]\displaystyle{ h }[/math] >> [math]\displaystyle{ \lambda }[/math], [math]\displaystyle{ kh }[/math] >> 1, and [math]\displaystyle{ \tanh (kh) = 1 }[/math].
- Shallow-water approximation is valid if the water depth is much less than a wavelength. In this case, [math]\displaystyle{ h \lt \lt \lambda }[/math], [math]\displaystyle{ kh }[/math] << 1, and [math]\displaystyle{ \tanh (kh) = kh }[/math].
For these two limits of water depth compared with wavelength the dispersion relation reduces to: [math]\displaystyle{ \omega^2 = g k \,\! }[/math] for [math]\displaystyle{ h \gt \lambda / 4 }[/math] for the Deep-water dispersion relation and [math]\displaystyle{ \omega^2 = g k^2 h }[/math], [math]\displaystyle{ h \lt \lambda / 11 }[/math] for the Shallow-water dispersion relation.
The stated limits for [math]\displaystyle{ h / \lambda }[/math] give a dispersion relation accurate within 10%. Because many wave properties can be measured with accuracies of 5-10%, the approximations are useful for calculating wave properties. Later we will learn to calculate wave properties as the waves propagate from deep to shallow water.
Phase Velocity
The phase velocity c is the speed at which a particular phase of the wave propagates, for example, the speed of propagation of the wave crest. In one wave period [math]\displaystyle{ T }[/math] the crest advances one wave-length \lambda and the phase speed is [math]\displaystyle{ c = \lambda / T = \omega / k }[/math]. Thus, the definition of phase speed is:
The direction of propagation is perpendicular to the wave crest and toward the positive [math]\displaystyle{ x- }[/math]direction. The deep- and shallow-water approximations for the dispersion relation give:
The approximations are accurate to about 5% for limits stated above.
In deep water, the phase speed depends on wave-length or wave frequency. Longer waves travel faster. Thus, deep-water waves are said to be dispersive. In shallow water, the phase speed is independent of the wave; it depends only on the depth of the water. Shallow-water waves are non-dispersive.
Group Velocity
The concept of group velocity [math]\displaystyle{ c_g }[/math] is fundamental for understanding the propagation of linear and nonlinear waves. First, it is the velocity at which a group of waves travels across the ocean. More importantly, it is also the propagation velocity of wave energy. Whitham 1974 ( §1.3 and §11.6) gives a clear derivation of the concept and the fundamental equation.
The definition of group velocity in two dimensions is:
Using the approximations for the dispersion relation:
For ocean-surface waves, the direction of propagation is perpendicular to the wave crests in the positive x direction. In the more general case of other types of waves, such as Kelvin and Rossby waves, the group velocity is not necessarily in the direction perpendicular to wave crests.
Notice that a group of deep-water waves moves at half the phase speed of the waves making up the group. How can this happen? If we could watch closely a group of waves crossing the sea, we would see waves crests appear at the back of the wave train, move through the train, and disappear at the leading edge of the group.
Each wave crest moves at twice the speed of the group. Do real ocean waves move in groups governed by the dispersion relation? Yes. Munk et al. 1963 in a remarkable series of experiments in the 1960s showed that ocean waves propagating over great distances are dispersive, and that the dispersion could be used to track storms. They recorded waves for many days using an array of three pressure gauges just offshore of San Clemente Island, 60 miles due west of San Diego, California. Wave spectra were calculated for each day's data. (The concept of a spectra is discussed below.) From the spectra, the amplitudes and frequencies of the low-frequency waves and the propagation direction of the waves were calculated. Finally, they plotted contours of wave energy on a frequency-time diagram (Figure 1).
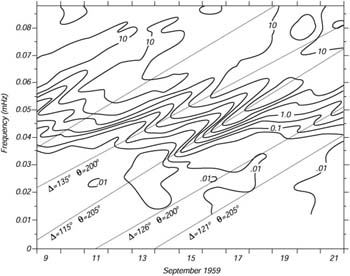
To understand the figure, consider a distant storm that produces waves of many frequencies. The lowest-frequency waves (smallest w) travel the fastest and they arrive before other, higher-frequency waves. The further away the storm, the longer the delay between arrivals of waves of different frequencies. The ridges of high wave energy seen in the Figure are produced by individual storm [math]\displaystyle{ \theta }[/math]. The slope of the ridge gives the distance to the storm in degrees [math]\displaystyle{ \Delta }[/math] along a great circle; and the phase information from the array gives the angle to the storm. The two angles give the storm's location relative to San Clemente. Thus waves arriving from 15 to 18 September produce a ridge indicating the storm was 115° away at an angle of 205° which is south of new Zealand near Antarctica.
The locations of the storms producing the waves recorded from June through October 1959 were compared with the location of storms plotted on weather maps and in most cases the two agreed well.
Wave Energy
The wave energy density [math]\displaystyle{ E }[/math] in Joules per square meter is related to the variance of sea-surface displacement [math]\displaystyle{ \zeta }[/math] by:
where [math]\displaystyle{ p_w }[/math] is water density, [math]\displaystyle{ g }[/math] is gravity, and the brackets denote a time average. Note that this formula requires that there is quasi steady state so that the average kinetic and potential energies are equal and is only valid for linear waves. Although the formula in theory will give different energy densities for different locations (e.g. for a standing wave there will be locations where the displacement, hence also the energy density, will always be zero), it will in practice give a good result which doesn't vary much from location to location.
Significant Wave-Height
What do we mean by wave-height? If we look at a wind-driven sea, we see waves of various heights. Some are much larger than most, others are much smaller (Figure 2). A practical definition that is often used is the height of the highest 1/3 of the waves, [math]\displaystyle{ H_{1/3} }[/math]. The height is computed as follows: measure wave-height for a few minutes, pick out say 120 wave crests and record their heights. Pick the 40 largest waves and calculate the average height of the 40 values. This is [math]\displaystyle{ H_{1/3} }[/math] for the wave record.
The concept of significant wave-height was developed during the World War II as part of a project to forecast ocean wave-heights and periods. Wiegel 1964: p. 198 reports that work at the Scripps Institution of Oceanography showed
... wave-height estimated by observers corresponds to the average of the highest 20 to 40 per cent of waves... Originally, the term significant wave-height was attached to the average of these observations, the highest 30 percent of the waves, but has evolved to become the average of the highest one-third of the waves, (designated [math]\displaystyle{ HS }[/math] or [math]\displaystyle{ H_{1/3} }[/math])
More recently, significant wave-height is calculated from measured wave displacement. If the sea contains a narrow range of wave frequencies, [math]\displaystyle{ H_{1/3} }[/math] is related to the standard deviation of sea-surface displacement (NAS 1963: 22; Hoffman and Karst 1975)
where [math]\displaystyle{ \lt \zeta^2 \gt ^{1/2} }[/math] is the standard deviation of surface displacement. This relationship is much more useful, and it is now the accepted way to calculate wave-height from wave measurements
Acknowledgment
The material in this page has come from Introduction to Physical Oceanography by Robert Stewart.