Burgers Equation

Nonlinear PDE's Course
Current Topic	Burgers Equation
Next Topic
Previous Topic	Reaction-Diffusion Systems

Introduction

We have already met the conservation law for the traffic equations

[math]\displaystyle{ \partial _{t}\rho +c\left( \rho \right) \partial _{x}\rho =0 }[/math]

and seen how this leads to shocks. We can smooth this equation by adding dispersion to the equation to give us

[math]\displaystyle{ \partial _{t}\rho +c\left( \rho \right) \partial _{x}\rho =\nu \partial _{x}^{2}\rho }[/math]

where [math]\displaystyle{ \nu \gt 0. }[/math]

The simplest equation of this type is to write

[math]\displaystyle{ \partial _{t}u+u\partial _{x}u=\nu \partial _{x}^{2}u }[/math]

(changing variables to [math]\displaystyle{ u }[/math] and this equation is known as Burgers equation.

Travelling Wave Solution

We can find a travelling wave solution by assuming that

[math]\displaystyle{ u\left( x,t\right) =u\left( x-ct\right) =u\left( \xi \right) }[/math]

This leads to the equations

[math]\displaystyle{ -cu^{\prime }+u^{\prime }u-\nu u^{\prime \prime }=0 }[/math]

We begin by looking at the phase plane for this system, writing [math]\displaystyle{ w=u^{\prime } }[/math] so that

[math]\displaystyle{ \begin{matrix} \dfrac{\mathrm{d}u}{\mathrm{d}\xi } &=&w \\ \dfrac{\mathrm{d}w}{\mathrm{d}\xi } &=&\frac{1}{\nu }\left( w\left( u-c\right) \right) \end{matrix} }[/math]

This is a degenerate system with the entire [math]\displaystyle{ u }[/math] axis being equilibria.

We can also solve this equation exactly as follows.

[math]\displaystyle{ -cu^{\prime }+u^{\prime }u-\nu u^{\prime \prime }=0 }[/math]

can be integrated to give

[math]\displaystyle{ -cu+\frac{1}{2}\left( u\right) ^{2}-\nu u^{\prime} =c_{1} }[/math]

which can be rearranged to give

[math]\displaystyle{ u^{\prime }=\frac{1}{2\nu }\left( \left( u\right) ^{2}-2cu-2c_{1}\right) }[/math]

We define the two roots of the quadratic [math]\displaystyle{ \left( u\right) ^{2}-2\nu u-2c_{1}=0 }[/math] by [math]\displaystyle{ u_{1} }[/math] and [math]\displaystyle{ u_{2} }[/math] and we assume that [math]\displaystyle{ u_{2} \lt u_{1} }[/math]. Note that there is only a bounded solution if we have two real roots and for the bounded solution [math]\displaystyle{ u_{2} \lt u \lt u_{1} }[/math]. We note that the wave speed is

[math]\displaystyle{ c=\frac{1}{2}\left( u_{1}+u_{2}\right) }[/math]

The equation can therefore be written as

[math]\displaystyle{ 2\nu u^{\prime }=\left( u-u_{1}\right) \left( u-u_{2}\right) }[/math]

which has solution

[math]\displaystyle{ u\left( \xi \right) =\frac{1}{2}\left( u_{1}+u_{2}\right) -\frac{1}{2}\left( u_{1}-u_{2}\right) \tanh \left[ \left( \frac{\xi }{4\nu }\right) \left( u_{1}-u_{2}\right) \right] }[/math]

Numerical Solution of Burgers equation

We can solve the equation using our split step spectral method. The equation can be written as

[math]\displaystyle{ \partial _{t}u=-\frac{1}{2}\partial _{x}\left( u^{2}\right) +\nu \partial _{x}^{2}u }[/math]

We solve this by solving in Fourier space to give

[math]\displaystyle{ \partial _{t}\hat{u}=-\frac{1}{2}ik \widehat{\left( u^{2}\right)} -\nu k^{2}\hat{u} }[/math]

Then we solve each of the steps in turn for a small time interval to give

[math]\displaystyle{ \begin{matrix} \tilde{u}\left( k,t+\Delta t\right) &=&\hat{u}\left( k,t\right) -\frac{ \Delta t}{2}ik\mathcal{F}\left( \left[ \mathcal{F}^{-1}\hat{u}\left( k,t\right) \right] ^{2}\right) \\ \hat{u}\left( k,t+\Delta t\right) &=&\tilde{u}\left( k,t+\Delta t\right) \exp \left( -\nu k^{2}\Delta t\right) \end{matrix} }[/math]

Phase plane for a travelling wave solution	Numerical solution of Burgers equation
Phase plane for a travelling wave solution of Burgers equation	Numerical solution of Burgers equation

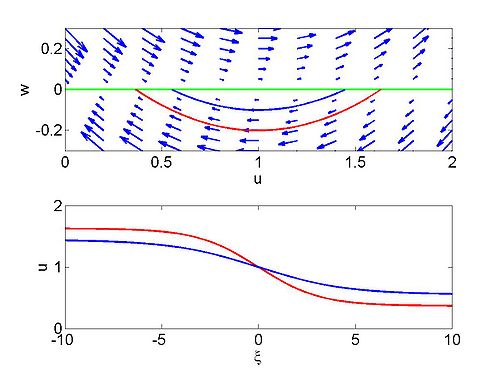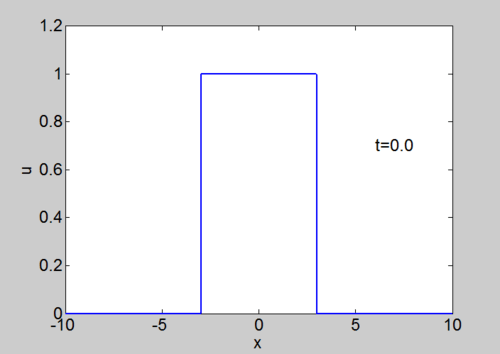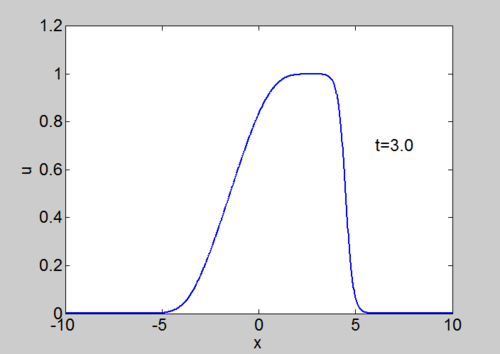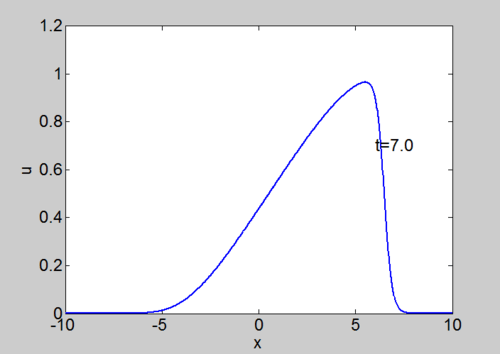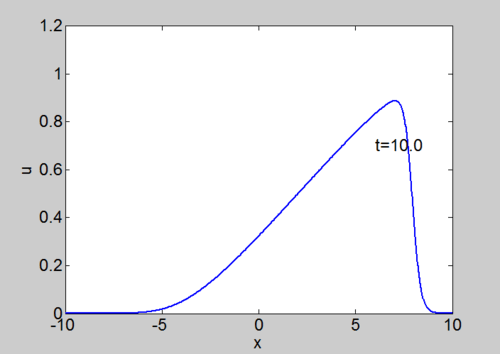Exact Solution of Burgers equations

We can find an exact solution to Burgers equation. We want to solve

[math]\displaystyle{ \begin{matrix} \partial _{t}u+u\partial _{x}u &=&\nu \partial _{x}^{2}u \\ u\left( x,0\right) &=&F\left( x\right) \end{matrix} }[/math]

Frist we write the equation as

[math]\displaystyle{ \partial _{t}u+\partial _{x}\left( \frac{u^{2}}{2}-\nu \partial _{x}u\right) =0 }[/math]

We want to find a function [math]\displaystyle{ \psi \left( x,t\right) }[/math] such that

[math]\displaystyle{ \partial _{x}\psi =u,\ \ \partial _{t}\psi =\nu \partial _{x}u-\frac{u^{2}}{2 } }[/math]

Note that because [math]\displaystyle{ \partial _{x}\partial _{t}\psi =\partial _{t}\partial _{x}\psi }[/math] we will satisfy Burgers equation. This gives us the following equation for [math]\displaystyle{ \psi }[/math]

[math]\displaystyle{ \partial _{t}\psi =\nu \partial _{x}^{2}\psi -\frac{1}{2}\left( \partial _{x}\psi \right) ^{2} }[/math]

We introduce the Cole-Hopf transformation

[math]\displaystyle{ \psi =-2\nu \log \left( \phi \right) }[/math]

From this we can obtain the three results:

[math]\displaystyle{ \begin{align} \partial _{x}\psi &=-2\nu \frac{\partial _{x}\phi }{\phi } \\ \partial _{x}^{2}\psi &=2\nu \left( \frac{\partial _{x}\phi }{\phi }\right) ^{2}-\frac{2\nu }{\phi }\partial _{x}^{2}\phi \\ \partial _{t}\psi &=-2\nu \frac{\partial _{t}\phi }{\phi } \end{align} }[/math]

Therefore

[math]\displaystyle{ \partial _{t}\psi =\nu \partial _{x}^{2}\psi -\frac{1}{2}\left( \partial _{x}\psi \right) ^{2} }[/math]

becomes

[math]\displaystyle{ -2\nu \frac{\partial _{t}\phi }{\phi }=2\nu ^{2}\left( \frac{\partial _{x}\phi }{\phi }\right) ^{2} -2\nu^2 \frac{\partial_x^2\phi}{\phi} -\frac{1}{2}\left( 2\nu \frac{\partial _{x}\phi }{\phi }\right) ^{2} }[/math]

or

[math]\displaystyle{ \partial _{t}\phi =\nu \partial _{x}^{2}\phi }[/math]

which is just the diffusion equation. Note that we also have to transform the boundary conditions. We have

[math]\displaystyle{ F\left( x\right) =u\left( x,0\right) =-2\nu \frac{\partial _{x}\phi \left( x,0\right) }{\phi \left( x,0\right) } }[/math]

We can write this as

[math]\displaystyle{ \frac{\mathrm{d}}{\mathrm{d}x}\left( \log \left( \phi \right) \right) =-\frac{1}{2\nu }F\left( x\right) }[/math]

which has solution

[math]\displaystyle{ \phi \left( x,0\right) =\Phi \left( x\right) =\exp \left( -\frac{1}{2\nu } \int_{0}^{x}F\left( s\right) \mathrm{d}s\right) }[/math]

We need to solve

[math]\displaystyle{ \begin{matrix} \partial _{t}\phi &=&\nu \partial _{x}^{2}\phi \\ \phi \left( x,0\right) &=&\Phi \left( x\right) \end{matrix} }[/math]

We take the Fourier transform and obtain

[math]\displaystyle{ \begin{matrix} \partial _{t}\hat{\phi} &=&-k^{2}\nu \hat{\phi} \\ \hat{\phi}\left( k,0\right) &=&\hat{\Phi}\left( k\right) \end{matrix} }[/math]

which has solution

[math]\displaystyle{ \hat{\phi}\left( k,t\right) =\hat{\Phi}\left( k\right) e^{-k^{2}\nu t} }[/math]

We can then use the convolution theorem to write

[math]\displaystyle{ \begin{matrix} \phi \left( x,t\right) &=&\Phi \left( x\right) * \mathcal{F}^{-1}\left[ e^{-k^{2}\nu t}\right] \\ &=&\frac{1}{2\sqrt{\pi \nu t}}\int_{-\infty }^{\infty }\Phi \left( y\right) \exp \left[ -\frac{\left( x-y\right) ^{2}}{4\nu t}\right] \mathrm{d}y \end{matrix} }[/math]

Which can be expressed as

[math]\displaystyle{ \phi \left( x,t\right) =\frac{1}{2\sqrt{\pi \nu t}}\int_{-\infty }^{\infty }\exp \left[ -\frac{f}{2\nu }\right] \mathrm{d}y }[/math]

where

[math]\displaystyle{ f\left( x,y,t\right) =\frac{1}{2\nu }\int_{0}^{y}F\left( s\right) \mathrm{d}s+\frac{ \left( x-y\right) ^{2}}{2t} }[/math]

To find [math]\displaystyle{ u }[/math] we recall that

[math]\displaystyle{ \begin{matrix} u\left( x,t\right) &=&-2\nu \dfrac{\partial _{x}\phi \left( x,t\right) }{\phi \left( x,t\right) } \\ &=&\dfrac{\int_{-\infty }^{\infty }\left( \frac{x-y}{t}\right) \exp \left[ - \dfrac{f}{2\nu }\right] \mathrm{d}y}{\int_{-\infty }^{\infty }\exp \left[ -\frac{f}{ 2\nu }\right] \mathrm{d}y} \end{matrix} }[/math]

Lecture Videos

Part 1

Load video

YouTube

YouTube might collect personal data. Privacy Policy

ContinueDismiss

Part 2

Load video

YouTube

YouTube might collect personal data. Privacy Policy

ContinueDismiss

Part 3

Load video

YouTube

YouTube might collect personal data. Privacy Policy

ContinueDismiss

Part 4

Load video

YouTube

YouTube might collect personal data. Privacy Policy

ContinueDismiss

Part 5

Load video

YouTube

YouTube might collect personal data. Privacy Policy

ContinueDismiss