Template:Derivation of reflection and transmission in two dimensions: Difference between revisions
No edit summary |
No edit summary |
||
| Line 14: | Line 14: | ||
<center><math> | <center><math> | ||
\phi_0(0) \int_{-L}^{L} e^{k_0 x} \left(\alpha \phi(x) - \partial_n \phi(x)\right)\mathrm{d}x | \phi_0(0) \int_{-L}^{L} e^{k_0 x} \left(\alpha \phi(x) - \partial_n \phi(x)\right)\mathrm{d}x | ||
+ 2k_0 R \int_{-h}^{0} \left(\phi_0(z)\right)^2 \mathrm{d}z = 0 | |||
</math></center> | </math></center> | ||
Therefore | Therefore | ||
<center><math> | <center><math> | ||
R = \frac{\int_{-L}^{L} e^{k_0 x} \left(\alpha \phi(x) - \partial_n \phi(x)\right)\mathrm{d}x } | R = -\frac{\int_{-L}^{L} e^{k_0 x} \left(\alpha \phi(x) - \partial_n \phi(x)\right)\mathrm{d}x } | ||
{2 k_0 \int_{-h}^{0} \left(\phi_0(z)\right)^2 \mathrm{d}z}. | {2 k_0 \int_{-h}^{0} \left(\phi_0(z)\right)^2 \mathrm{d}z}. | ||
</math></center> | </math></center> | ||
and using a wave incident from the right we obtain | and using a wave incident from the right we obtain | ||
<center><math> | <center><math> | ||
T = 1 - \frac{\int_{-L}^{L} e^{-k_0 x} \left(\alpha \phi(x) - \partial_n \phi(x)\right)\mathrm{d}x } | |||
{2 k_0 \int_{-h}^{0} \left(\phi_0(z)\right)^2 \mathrm{d}z}. | {2 k_0 \int_{-h}^{0} \left(\phi_0(z)\right)^2 \mathrm{d}z}. | ||
</math></center> | </math></center> | ||
Note that an expression for the integral in the denominator can be found in | |||
[[Eigenfunction Matching for a Semi-Infinite Dock]] | |||
Revision as of 09:08, 27 November 2009
The Reflection and Transmission Coefficients represent the ratio of the amplitude of the reflected or transmitted wave to the amplitude of the incident wave. Conservation of energy means that [math]\displaystyle{ |R|^2+|T|^2=1\, }[/math].
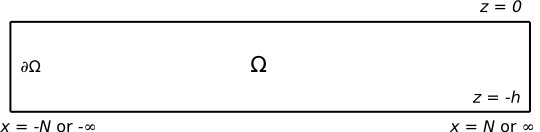
We can calculate the Reflection and Transmission coefficients by applying Green's theorem to [math]\displaystyle{ \phi\, }[/math] and [math]\displaystyle{ \phi^{\mathrm{I}}\, }[/math] [math]\displaystyle{ \phi^{\mathrm{I}}\, }[/math] is a plane wave travelling in the [math]\displaystyle{ x }[/math] direction,
where [math]\displaystyle{ A }[/math] is the wave amplitude (in potential) [math]\displaystyle{ \mathrm{i} k }[/math] is the positive imaginary solution of the Dispersion Relation for a Free Surface (note we are assuming that the time dependence is of the form [math]\displaystyle{ \exp(-\mathrm{i}\omega t) }[/math]) and
We assume that [math]\displaystyle{ A=1 }[/math]. This gives us
This means that (using the far field behaviour of the potential [math]\displaystyle{ \phi }[/math]
Therefore
and using a wave incident from the right we obtain
Note that an expression for the integral in the denominator can be found in Eigenfunction Matching for a Semi-Infinite Dock