Eigenfunction Matching for a Circular Floating Elastic Plate: Difference between revisions
No edit summary |
|||
| Line 15: | Line 15: | ||
upward with the water surface at <math>z=0</math> and the sea floor at <math>z=-H</math>. The | upward with the water surface at <math>z=0</math> and the sea floor at <math>z=-H</math>. The | ||
boundary value problem can therefore be expressed as | boundary value problem can therefore be expressed as | ||
<center> | |||
<math> | <math> | ||
\Delta\phi=0, \,\, -H<z<0, | \Delta\phi=0, \,\, -H<z<0, | ||
</math> | </math> | ||
</center> | |||
<center> | |||
<math> | <math> | ||
\phi_{z}=0, \,\, z=-H, | \phi_{z}=0, \,\, z=-H, | ||
</math> | </math> | ||
</center> | |||
<math> | <center><math> | ||
\phi_{z}=\alpha\phi, \,\, z=0,\,r>a, | \phi_{z}=\alpha\phi, \,\, z=0,\,r>a, | ||
</math> | </center></math> | ||
<center> | |||
<math> | <math> | ||
(\beta\Delta^{2}+1-\alpha\gamma)\phi_{z}=\alpha\phi, \,\, z=0,\,r<a | (\beta\Delta^{2}+1-\alpha\gamma)\phi_{z}=\alpha\phi, \,\, z=0,\,r<a | ||
</math> | </math> | ||
</center> | |||
where the constants <math>\beta</math> and <math>\gamma</math> are given by | where the constants <math>\beta</math> and <math>\gamma</math> are given by | ||
<center> | |||
<math> | <math> | ||
\beta=\frac{D}{\rho\,L^{4}g}, \gamma=\frac{\rho_{i}h}{\rho\,L} | \beta=\frac{D}{\rho\,L^{4}g}, \gamma=\frac{\rho_{i}h}{\rho\,L} | ||
</math> | </math> | ||
</center> | |||
and <math>\rho_{i}</math> is the density of the plate. We | and <math>\rho_{i}</math> is the density of the plate. We | ||
must also apply the edge conditions for the plate and the [[Sommerfeld Radiation Condition]] | must also apply the edge conditions for the plate and the [[Sommerfeld Radiation Condition]] | ||
| Line 49: | Line 50: | ||
We now separate variables, noting that since the problem has | We now separate variables, noting that since the problem has | ||
circular symmetry we can write the potential as | circular symmetry we can write the potential as | ||
<center> | |||
<math> | <math> | ||
\phi(r,\theta,z)=\zeta(z)\sum_{n=-\infty}^{\infty}\rho_{n}(r)e^{i n \theta} | \phi(r,\theta,z)=\zeta(z)\sum_{n=-\infty}^{\infty}\rho_{n}(r)e^{i n \theta} | ||
</math> | </math> | ||
</center> | |||
Applying Laplace's equation we obtain | Applying Laplace's equation we obtain | ||
<center> | |||
<math> | <math> | ||
\zeta_{zz}+\mu^{2}\zeta=0 | \zeta_{zz}+\mu^{2}\zeta=0 | ||
</math> | </math> | ||
</center> | |||
so that: | so that: | ||
<center> | |||
<math> | <math> | ||
\zeta=\cos\mu(z+H) | \zeta=\cos\mu(z+H) | ||
</math> | </math> | ||
</center> | |||
where the separation constant <math>\mu^{2}</math> must | where the separation constant <math>\mu^{2}</math> must | ||
satisfy the [[Dispersion Relation for a Free Surface]] | satisfy the [[Dispersion Relation for a Free Surface]] | ||
<center> | |||
<math> | <math> | ||
k\tan\left( kH\right) =-\alpha,\quad r>a\,\,\,(1) | k\tan\left( kH\right) =-\alpha,\quad r>a\,\,\,(1) | ||
</math> | </math> | ||
</center> | |||
and the [[Dispersion Relation for a Floating Elastic Plate]] | and the [[Dispersion Relation for a Floating Elastic Plate]] | ||
<center> | |||
<math> | <math> | ||
\kappa\tan(\kappa H)=\frac{-\alpha}{\beta\kappa^{4}+1-\alpha\gamma},\quad | \kappa\tan(\kappa H)=\frac{-\alpha}{\beta\kappa^{4}+1-\alpha\gamma},\quad | ||
r<a \,\,\,(2) | r<a \,\,\,(2) | ||
</math> | </math> | ||
</center> | |||
Note that we have set <math>\mu=k</math> under the free | Note that we have set <math>\mu=k</math> under the free | ||
surface and <math>\mu=\kappa</math> under the plate. We denote the | surface and <math>\mu=\kappa</math> under the plate. We denote the | ||
| Line 90: | Line 91: | ||
the negative imaginary solution is <math>\kappa_{0}</math> and the positive real | the negative imaginary solution is <math>\kappa_{0}</math> and the positive real | ||
solutions are <math>\kappa_{m}</math>, <math>m\geq1</math>. We define | solutions are <math>\kappa_{m}</math>, <math>m\geq1</math>. We define | ||
<center> | |||
<math> | <math> | ||
\phi_{m}\left( z\right) =\frac{\cos k_{m}(z+H)}{\cos k_{m}H},\quad m\geq0 | \phi_{m}\left( z\right) =\frac{\cos k_{m}(z+H)}{\cos k_{m}H},\quad m\geq0 | ||
</math> | </math> | ||
</center> | |||
as the vertical eigenfunction of the potential in the open | as the vertical eigenfunction of the potential in the open | ||
water region and | water region and | ||
<center> | |||
<math> | <math> | ||
\psi_{m}\left( z\right) =\frac{\cos\kappa_{m}(z+H)}{\cos\kappa_{m}H},\quad | \psi_{m}\left( z\right) =\frac{\cos\kappa_{m}(z+H)}{\cos\kappa_{m}H},\quad | ||
m\geq-2 | m\geq-2 | ||
</math> | </math> | ||
</center> | |||
as the vertical eigenfunction of the potential in the plate | as the vertical eigenfunction of the potential in the plate | ||
covered region. For later reference, we note that: | covered region. For later reference, we note that: | ||
<center> | |||
<math> | <math> | ||
\int\nolimits_{-H}^{0}\phi_{m}(z)\phi_{n}(z) d z=A_{m}\delta_{mn} | \int\nolimits_{-H}^{0}\phi_{m}(z)\phi_{n}(z) d z=A_{m}\delta_{mn} | ||
</math> | </math> | ||
</center> | |||
where | where | ||
<center> | |||
<math> | <math> | ||
A_{m}=\frac{1}{2}\left( \frac{\cos k_{m}H\sin k_{m}H+k_{m}H}{k_{m}\cos | A_{m}=\frac{1}{2}\left( \frac{\cos k_{m}H\sin k_{m}H+k_{m}H}{k_{m}\cos | ||
^{2}k_{m}H}\right) | ^{2}k_{m}H}\right) | ||
</math> | </math> | ||
</center> | |||
and | and | ||
<center> | |||
<math> | <math> | ||
\int\nolimits_{-H}^{0}\phi_{n}(z)\psi_{m}(z) d z=B_{mn} | \int\nolimits_{-H}^{0}\phi_{n}(z)\psi_{m}(z) d z=B_{mn} | ||
</math> | </math> | ||
</center> | |||
where | where | ||
<math> | <center><math> | ||
B_{mn}=\frac{k_{n}\sin k_{n}H\cos\kappa_{m}H-\kappa_{m}\cos k_{n}H\sin | B_{mn}=\frac{k_{n}\sin k_{n}H\cos\kappa_{m}H-\kappa_{m}\cos k_{n}H\sin | ||
\kappa_{m}H}{\left( \cos k_{n}H\cos\kappa_{m}H\right) \left( k_{n} | \kappa_{m}H}{\left( \cos k_{n}H\cos\kappa_{m}H\right) \left( k_{n} | ||
^{2}-\kappa_{m}^{2}\right) } | ^{2}-\kappa_{m}^{2}\right) } | ||
</math> | </center></math> | ||
We now solve for the function <math>\rho_{n}(r)</math>. | We now solve for the function <math>\rho_{n}(r)</math>. | ||
Using Laplace's equation in polar coordinates we obtain | Using Laplace's equation in polar coordinates we obtain | ||
<center> | |||
<math> | <math> | ||
\frac{\mathrm{d}^{2}\rho_{n}}{\mathrm{d}r^{2}}+\frac{1}{r} | \frac{\mathrm{d}^{2}\rho_{n}}{\mathrm{d}r^{2}}+\frac{1}{r} | ||
| Line 139: | Line 139: | ||
\frac{n^{2}}{r^{2}}+\mu^{2}\right) \rho_{n}=0 | \frac{n^{2}}{r^{2}}+\mu^{2}\right) \rho_{n}=0 | ||
</math> | </math> | ||
</center> | |||
where <math>\mu</math> is <math>k_{m}</math> or | where <math>\mu</math> is <math>k_{m}</math> or | ||
<math>\kappa_{m},</math> depending on whether <math>r</math> is | <math>\kappa_{m},</math> depending on whether <math>r</math> is | ||
greater or less than <math>a</math>. We can convert this equation to the | greater or less than <math>a</math>. We can convert this equation to the | ||
standard form by substituting <math>y=\mu r</math> to obtain | standard form by substituting <math>y=\mu r</math> to obtain | ||
<center> | |||
<math> | <math> | ||
y^{2}\frac{\mathrm{d}^{2}\rho_{n}}{\mathrm{d}y^{2}}+y\frac{\mathrm{d}\rho_{n} | y^{2}\frac{\mathrm{d}^{2}\rho_{n}}{\mathrm{d}y^{2}}+y\frac{\mathrm{d}\rho_{n} | ||
}{\rm{d}y}-(n^{2}+y^{2})\rho_{n}=0 | }{\rm{d}y}-(n^{2}+y^{2})\rho_{n}=0 | ||
</math> | </math> | ||
</center> | |||
The solution of this equation is a linear combination of the | The solution of this equation is a linear combination of the | ||
modified Bessel functions of order <math>n</math>, <math>I_{n}(y)</math> and | modified Bessel functions of order <math>n</math>, <math>I_{n}(y)</math> and | ||
| Line 157: | Line 157: | ||
linear combination of <math>K_{n}(y)</math>. Therefore the potential can | linear combination of <math>K_{n}(y)</math>. Therefore the potential can | ||
be expanded as | be expanded as | ||
<center> | |||
<math> | <math> | ||
\phi(r,\theta,z)=\sum_{n=-\infty}^{\infty}\sum_{m=0}^{\infty}a_{mn}K_{n} | \phi(r,\theta,z)=\sum_{n=-\infty}^{\infty}\sum_{m=0}^{\infty}a_{mn}K_{n} | ||
(k_{m}r)e^{i n\theta}\phi_{m}(z), \;\;r>a | (k_{m}r)e^{i n\theta}\phi_{m}(z), \;\;r>a | ||
</math> | </math> | ||
</center> | |||
and | and | ||
<center> | |||
<math> | <math> | ||
\phi(r,\theta,z)=\sum_{n=-\infty}^{\infty}\sum_{m=-2}^{\infty}b_{mn} | \phi(r,\theta,z)=\sum_{n=-\infty}^{\infty}\sum_{m=-2}^{\infty}b_{mn} | ||
I_{n}(\kappa_{m}r)e^{i n\theta}\psi_{m}(z), \;\;r<a | I_{n}(\kappa_{m}r)e^{i n\theta}\psi_{m}(z), \;\;r<a | ||
</math> | </math> | ||
</center> | |||
where <math>a_{mn}</math> and <math>b_{mn}</math> | where <math>a_{mn}</math> and <math>b_{mn}</math> | ||
are the coefficients of the potential in the open water and | are the coefficients of the potential in the open water and | ||
| Line 179: | Line 179: | ||
in displacement travelling in the positive <math>x</math>-direction. | in displacement travelling in the positive <math>x</math>-direction. | ||
The incident potential can therefore be written as | The incident potential can therefore be written as | ||
<center> | |||
<math> | <math> | ||
\phi^{\mathrm{I}} =\frac{A}{i\sqrt{\alpha}}e^{k_{0}x}\phi_{0}\left( | \phi^{\mathrm{I}} =\frac{A}{i\sqrt{\alpha}}e^{k_{0}x}\phi_{0}\left( | ||
| Line 186: | Line 186: | ||
e^{i n \theta} | e^{i n \theta} | ||
</math> | </math> | ||
</center> | |||
where <math>e_{n}=A/\left(i\sqrt{\alpha}\right)</math> | where <math>e_{n}=A/\left(i\sqrt{\alpha}\right)</math> | ||
(we retain the dependence on <math>n</math> for situations | (we retain the dependence on <math>n</math> for situations | ||
| Line 196: | Line 196: | ||
considered. The vertical force and bending moment must vanish, which can be | considered. The vertical force and bending moment must vanish, which can be | ||
written as | written as | ||
<center> | |||
<math> | <math> | ||
\left[\bar{\Delta}-\frac{1-\nu}{r}\left(\frac{\partial}{\partial r} | \left[\bar{\Delta}-\frac{1-\nu}{r}\left(\frac{\partial}{\partial r} | ||
| Line 202: | Line 202: | ||
w=0\,\,\,(3) | w=0\,\,\,(3) | ||
</math> | </math> | ||
</center> | |||
and | and | ||
<center> | |||
<math> | <math> | ||
\left[ \frac{\partial}{\partial r}\bar{\Delta}-\frac{1-\nu}{r^{2}}\left( | \left[ \frac{\partial}{\partial r}\bar{\Delta}-\frac{1-\nu}{r^{2}}\left( | ||
| Line 210: | Line 210: | ||
{\partial\theta^{2}}\right] w=0 \,\,\,(4) | {\partial\theta^{2}}\right] w=0 \,\,\,(4) | ||
</math> | </math> | ||
</center> | |||
where <math>w</math> is the time-independent surface | where <math>w</math> is the time-independent surface | ||
displacement, <math>\nu</math> is Poisson's ratio, and <math>\bar{\Delta}</math> is the | displacement, <math>\nu</math> is Poisson's ratio, and <math>\bar{\Delta}</math> is the | ||
polar coordinate Laplacian | polar coordinate Laplacian | ||
<center> | |||
<math> | <math> | ||
\bar{\Delta}=\frac{\partial^{2}}{\partial r^{2}}+\frac{1}{r}\frac{\partial | \bar{\Delta}=\frac{\partial^{2}}{\partial r^{2}}+\frac{1}{r}\frac{\partial | ||
}{\partial r}+\frac{1}{r^{2}}\frac{\partial^{2}}{\partial\theta^{2}} | }{\partial r}+\frac{1}{r^{2}}\frac{\partial^{2}}{\partial\theta^{2}} | ||
</math> | </math> | ||
</center> | |||
== Displacement of the plate == | == Displacement of the plate == | ||
The surface displacement and the water velocity potential at | The surface displacement and the water velocity potential at | ||
the water surface are linked through the kinematic boundary condition | the water surface are linked through the kinematic boundary condition | ||
<center> | |||
<math> | <math> | ||
\phi_{z}=-i\sqrt{\alpha}w,\,\,\,z=0 | \phi_{z}=-i\sqrt{\alpha}w,\,\,\,z=0 | ||
</math> | </math> | ||
</center> | |||
From equations (\ref{bvp_plate}) the potential and the surface | From equations (\ref{bvp_plate}) the potential and the surface | ||
displacement are therefore related by | displacement are therefore related by | ||
<center> | |||
<math> | <math> | ||
w=i\sqrt{\alpha}\phi,\quad r>a | w=i\sqrt{\alpha}\phi,\quad r>a | ||
</math> | </math> | ||
</center> | |||
and | and | ||
<center> | |||
<math> | <math> | ||
(\beta\bar{\Delta}^{2}+1-\alpha\gamma)w=i\sqrt{\alpha}\phi,\quad r<a | (\beta\bar{\Delta}^{2}+1-\alpha\gamma)w=i\sqrt{\alpha}\phi,\quad r<a | ||
</math> | </math> | ||
</center> | |||
The surface displacement can also be expanded in eigenfunctions | The surface displacement can also be expanded in eigenfunctions | ||
as | as | ||
| Line 260: | Line 260: | ||
using the fact that | using the fact that | ||
<center> | |||
<math> | <math> | ||
\bar{\Delta}\left( I_{n}(\kappa_{m}r)e^{i n\theta}\right) =\kappa_{m} | \bar{\Delta}\left( I_{n}(\kappa_{m}r)e^{i n\theta}\right) =\kappa_{m} | ||
^{2}I_{n}(\kappa_{m}r)e^{i n\theta}\,\,\,(5) | ^{2}I_{n}(\kappa_{m}r)e^{i n\theta}\,\,\,(5) | ||
</math> | </math> | ||
</center> | |||
==An infinite dimensional system of equations== | ==An infinite dimensional system of equations== | ||
| Line 272: | Line 272: | ||
using (5). Since the angular modes are uncoupled the | using (5). Since the angular modes are uncoupled the | ||
conditions apply to each mode, giving | conditions apply to each mode, giving | ||
<center> | |||
<math> | <math> | ||
\sum_{m=-2}^{\infty}(\beta\kappa_{m}^{4}+1-\alpha\gamma)^{-1}b_{mn} | \sum_{m=-2}^{\infty}(\beta\kappa_{m}^{4}+1-\alpha\gamma)^{-1}b_{mn} | ||
| Line 279: | Line 279: | ||
\right) =0\,\,\,(6) | \right) =0\,\,\,(6) | ||
</math> | </math> | ||
</center> | |||
<center> | |||
<math> | <math> | ||
\sum_{m=-2}^{\infty}(\beta\kappa_{m}^{4}+1-\alpha\gamma)^{-1}b_{mn} | \sum_{m=-2}^{\infty}(\beta\kappa_{m}^{4}+1-\alpha\gamma)^{-1}b_{mn} | ||
| Line 287: | Line 288: | ||
=0\,\,\,(7) | =0\,\,\,(7) | ||
</math> | </math> | ||
</center> | |||
The potential and its derivative must be continuous across the | The potential and its derivative must be continuous across the | ||
transition from open water to the plate covered region. Therefore, the | transition from open water to the plate covered region. Therefore, the | ||
potentials and their derivatives at <math>r=a</math> have to be equal. | potentials and their derivatives at <math>r=a</math> have to be equal. | ||
Again we know that this must be true for each angle and we obtain | Again we know that this must be true for each angle and we obtain | ||
<center> | |||
<math> | <math> | ||
e_{n}I_{n}(k_{0}a)\phi_{0}\left( z\right) + \sum_{m=0}^{\infty} | e_{n}I_{n}(k_{0}a)\phi_{0}\left( z\right) + \sum_{m=0}^{\infty} | ||
| Line 298: | Line 299: | ||
=\sum_{m=-2}^{\infty}b_{mn}I_{n}(\kappa_{m}a)\psi_{m}(z) | =\sum_{m=-2}^{\infty}b_{mn}I_{n}(\kappa_{m}a)\psi_{m}(z) | ||
</math> | </math> | ||
</center> | |||
and | and | ||
<center> | |||
<math> | <math> | ||
e_{n}k_{0}I_{n}^{\prime}(k_{0}a)\phi_{0}\left( z\right) +\sum | e_{n}k_{0}I_{n}^{\prime}(k_{0}a)\phi_{0}\left( z\right) +\sum | ||
| Line 307: | Line 308: | ||
_{m}(z) | _{m}(z) | ||
</math> | </math> | ||
</center> | |||
for each <math>n</math>. | for each <math>n</math>. | ||
We solve these equations by multiplying both equations by | We solve these equations by multiplying both equations by | ||
<math>\phi_{l}(z)</math> and integrating from <math>-H</math> to <math>0</math> to obtain: | <math>\phi_{l}(z)</math> and integrating from <math>-H</math> to <math>0</math> to obtain: | ||
<center> | |||
<math> | <math> | ||
e_{n}I_{n}(k_{0}a)A_{0}\delta_{0l}+a_{ln}K_{n}(k_{l}a)A_{l} | e_{n}I_{n}(k_{0}a)A_{0}\delta_{0l}+a_{ln}K_{n}(k_{l}a)A_{l} | ||
=\sum_{m=-2}^{\infty}b_{mn}I_{n}(\kappa_{m}a)B_{ml} \,\,\,(8) | =\sum_{m=-2}^{\infty}b_{mn}I_{n}(\kappa_{m}a)B_{ml} \,\,\,(8) | ||
</math> | </math> | ||
</center> | |||
and | and | ||
<center> | |||
<math> | <math> | ||
e_{n}k_{0}I_{n}^{\prime}(k_{0}a)A_{0}\delta_{0l}+a_{ln}k_{l}K_{n}^{\prime | e_{n}k_{0}I_{n}^{\prime}(k_{0}a)A_{0}\delta_{0l}+a_{ln}k_{l}K_{n}^{\prime | ||
| Line 325: | Line 326: | ||
a)B_{ml} \,\,\,(9) | a)B_{ml} \,\,\,(9) | ||
</math> | </math> | ||
</center> | |||
Equation (8) can be solved for the open water | Equation (8) can be solved for the open water | ||
coefficients <math>a_{mn}</math> | coefficients <math>a_{mn}</math> | ||
<center> | |||
<math> | <math> | ||
a_{ln}=-e_{n}\frac{I_{n}(k_{0}a)}{K_{n}(k_{0}a)}\delta_{0l}+\sum | a_{ln}=-e_{n}\frac{I_{n}(k_{0}a)}{K_{n}(k_{0}a)}\delta_{0l}+\sum | ||
_{m=-2}^{\infty}b_{mn}\frac{I_{n}(\kappa_{m}a)B_{ml}}{K_{n}(k_{l}a)A_{l}} | _{m=-2}^{\infty}b_{mn}\frac{I_{n}(\kappa_{m}a)B_{ml}}{K_{n}(k_{l}a)A_{l}} | ||
</math> | </math> | ||
</center> | |||
which can then be substituted into equation | which can then be substituted into equation | ||
(9) to give us | (9) to give us | ||
<center> | |||
<math> | <math> | ||
\left( k_{0}I_{n}^{\prime}(k_{0}a)-k_{0}\frac{K_{n}^{\prime}(k_{0} | \left( k_{0}I_{n}^{\prime}(k_{0}a)-k_{0}\frac{K_{n}^{\prime}(k_{0} | ||
| Line 344: | Line 345: | ||
_{m}a)\right) B_{ml}b_{mn}\,\,\,(10) | _{m}a)\right) B_{ml}b_{mn}\,\,\,(10) | ||
</math> | </math> | ||
</center> | |||
for each <math>n</math>. | for each <math>n</math>. | ||
Together with equations (6) and (7) | Together with equations (6) and (7) | ||
| Line 356: | Line 357: | ||
be <math>M</math>. We also set the angular expansion to be from | be <math>M</math>. We also set the angular expansion to be from | ||
<math>n=-N</math> to <math>N</math>. This gives us | <math>n=-N</math> to <math>N</math>. This gives us | ||
<center> | |||
<math> | <math> | ||
\phi(r,\theta,z)=\sum_{n=-N}^{N}\sum_{m=0}^{M}a_{mn}K_{n}(k_{m}r)e^{i | \phi(r,\theta,z)=\sum_{n=-N}^{N}\sum_{m=0}^{M}a_{mn}K_{n}(k_{m}r)e^{i | ||
n\theta }\phi_{m}(z), \;\;r>a | n\theta }\phi_{m}(z), \;\;r>a | ||
</math> | </math> | ||
</center> | |||
and | and | ||
<center> | |||
<math> | <math> | ||
\phi(r,\theta,z)=\sum_{n=-N}^{N}\sum_{m=-2}^{M}b_{mn}I_{n}(\kappa | \phi(r,\theta,z)=\sum_{n=-N}^{N}\sum_{m=-2}^{M}b_{mn}I_{n}(\kappa | ||
_{m}r)e^{i n\theta}\psi_{m}(z), \;\;r<a | _{m}r)e^{i n\theta}\psi_{m}(z), \;\;r<a | ||
</math> | </math> | ||
</center> | |||
Since <math>l</math> is an integer with <math>0\leq l\leq | Since <math>l</math> is an integer with <math>0\leq l\leq | ||
M</math> this leads to a system of <math>M+1</math> equations. | M</math> this leads to a system of <math>M+1</math> equations. | ||
| Line 374: | Line 375: | ||
are obtained from the boundary conditions for the free plate (6) | are obtained from the boundary conditions for the free plate (6) | ||
and (7). The equations to be solved for each <math>n</math> are | and (7). The equations to be solved for each <math>n</math> are | ||
<center> | |||
<math> | <math> | ||
\left( k_{0}I_{n}^{\prime}(k_{0}a)-k_{0}\frac{K_{n}^{\prime}(k_{0} | \left( k_{0}I_{n}^{\prime}(k_{0}a)-k_{0}\frac{K_{n}^{\prime}(k_{0} | ||
| Line 382: | Line 383: | ||
B_{ml}b_{mn} | B_{ml}b_{mn} | ||
</math> | </math> | ||
</center> | |||
<center> | |||
<math> | <math> | ||
\sum_{m=-2}^{M}(\beta\kappa_{m}^{4}+1-\alpha\gamma)^{-1}b_{mn} | \sum_{m=-2}^{M}(\beta\kappa_{m}^{4}+1-\alpha\gamma)^{-1}b_{mn} | ||
| Line 389: | Line 391: | ||
\right) =0 | \right) =0 | ||
</math> | </math> | ||
</center> | |||
and | and | ||
<center> | |||
<math> | <math> | ||
\sum_{m=-2}^{M}(\beta\kappa_{m}^{4}+1-\alpha\gamma)^{-1}b_{mn} | \sum_{m=-2}^{M}(\beta\kappa_{m}^{4}+1-\alpha\gamma)^{-1}b_{mn} | ||
| Line 398: | Line 400: | ||
_{m}a)\right) \right) =0 | _{m}a)\right) \right) =0 | ||
</math> | </math> | ||
</center> | |||
It should be noted that the solutions for positive and negative | It should be noted that the solutions for positive and negative | ||
<math>n</math> are identical so that they do not both need to be | <math>n</math> are identical so that they do not both need to be | ||
Revision as of 02:06, 4 September 2006
Introduction
We show here a solution for a Floating Elastic Plate on Finite Depth water based on Peter, Meylan and Chung 2004. A solution for Shallow Depth was given in Zilman and Miloh 2000 and we will also show this.
Governing Equations
We begin with the Frequency Domain Problem for a Floating Elastic Plate in the non-dimensional form of Tayler 1986 (Dispersion Relation for a Floating Elastic Plate) We will use a cylindrical coordinate system, [math]\displaystyle{ (r,\theta,z) }[/math], assumed to have its origin at the centre of the circular plate which has radius [math]\displaystyle{ a }[/math]. The water is assumed to have constant finite depth [math]\displaystyle{ H }[/math] and the [math]\displaystyle{ z }[/math]-direction points vertically upward with the water surface at [math]\displaystyle{ z=0 }[/math] and the sea floor at [math]\displaystyle{ z=-H }[/math]. The boundary value problem can therefore be expressed as
[math]\displaystyle{ \Delta\phi=0, \,\, -H\lt z\lt 0, }[/math]
[math]\displaystyle{ \phi_{z}=0, \,\, z=-H, }[/math]
[math]\displaystyle{ (\beta\Delta^{2}+1-\alpha\gamma)\phi_{z}=\alpha\phi, \,\, z=0,\,r\lt a }[/math]
where the constants [math]\displaystyle{ \beta }[/math] and [math]\displaystyle{ \gamma }[/math] are given by
[math]\displaystyle{ \beta=\frac{D}{\rho\,L^{4}g}, \gamma=\frac{\rho_{i}h}{\rho\,L} }[/math]
and [math]\displaystyle{ \rho_{i} }[/math] is the density of the plate. We must also apply the edge conditions for the plate and the Sommerfeld Radiation Condition as [math]\displaystyle{ r\rightarrow\infty }[/math]. The subscript [math]\displaystyle{ z }[/math] denotes the derivative in [math]\displaystyle{ z }[/math]-direction.
Solution Method
Separation of variables
We now separate variables, noting that since the problem has circular symmetry we can write the potential as
[math]\displaystyle{ \phi(r,\theta,z)=\zeta(z)\sum_{n=-\infty}^{\infty}\rho_{n}(r)e^{i n \theta} }[/math]
Applying Laplace's equation we obtain
[math]\displaystyle{ \zeta_{zz}+\mu^{2}\zeta=0 }[/math]
so that:
[math]\displaystyle{ \zeta=\cos\mu(z+H) }[/math]
where the separation constant [math]\displaystyle{ \mu^{2} }[/math] must satisfy the Dispersion Relation for a Free Surface
[math]\displaystyle{ k\tan\left( kH\right) =-\alpha,\quad r\gt a\,\,\,(1) }[/math]
and the Dispersion Relation for a Floating Elastic Plate
[math]\displaystyle{ \kappa\tan(\kappa H)=\frac{-\alpha}{\beta\kappa^{4}+1-\alpha\gamma},\quad r\lt a \,\,\,(2) }[/math]
Note that we have set [math]\displaystyle{ \mu=k }[/math] under the free surface and [math]\displaystyle{ \mu=\kappa }[/math] under the plate. We denote the positive imaginary solution of (1) by [math]\displaystyle{ k_{0} }[/math] and the positive real solutions by [math]\displaystyle{ k_{m} }[/math], [math]\displaystyle{ m\geq1 }[/math]. The solutions of (2) will be denoted by [math]\displaystyle{ \kappa_{m} }[/math], [math]\displaystyle{ m\geq-2 }[/math]. The fully complex solutions with positive imaginary part are [math]\displaystyle{ \kappa_{-2} }[/math] and [math]\displaystyle{ \kappa_{-1} }[/math] (where [math]\displaystyle{ \kappa_{-1}=\overline{\kappa_{-2}} }[/math]), the negative imaginary solution is [math]\displaystyle{ \kappa_{0} }[/math] and the positive real solutions are [math]\displaystyle{ \kappa_{m} }[/math], [math]\displaystyle{ m\geq1 }[/math]. We define
[math]\displaystyle{ \phi_{m}\left( z\right) =\frac{\cos k_{m}(z+H)}{\cos k_{m}H},\quad m\geq0 }[/math]
as the vertical eigenfunction of the potential in the open water region and
[math]\displaystyle{ \psi_{m}\left( z\right) =\frac{\cos\kappa_{m}(z+H)}{\cos\kappa_{m}H},\quad m\geq-2 }[/math]
as the vertical eigenfunction of the potential in the plate covered region. For later reference, we note that:
[math]\displaystyle{ \int\nolimits_{-H}^{0}\phi_{m}(z)\phi_{n}(z) d z=A_{m}\delta_{mn} }[/math]
where
[math]\displaystyle{ A_{m}=\frac{1}{2}\left( \frac{\cos k_{m}H\sin k_{m}H+k_{m}H}{k_{m}\cos ^{2}k_{m}H}\right) }[/math]
and
[math]\displaystyle{ \int\nolimits_{-H}^{0}\phi_{n}(z)\psi_{m}(z) d z=B_{mn} }[/math]
where
We now solve for the function [math]\displaystyle{ \rho_{n}(r) }[/math]. Using Laplace's equation in polar coordinates we obtain
[math]\displaystyle{ \frac{\mathrm{d}^{2}\rho_{n}}{\mathrm{d}r^{2}}+\frac{1}{r} \frac{\mathrm{d}\rho_{n}}{\mathrm{d}r}-\left( \frac{n^{2}}{r^{2}}+\mu^{2}\right) \rho_{n}=0 }[/math]
where [math]\displaystyle{ \mu }[/math] is [math]\displaystyle{ k_{m} }[/math] or [math]\displaystyle{ \kappa_{m}, }[/math] depending on whether [math]\displaystyle{ r }[/math] is greater or less than [math]\displaystyle{ a }[/math]. We can convert this equation to the standard form by substituting [math]\displaystyle{ y=\mu r }[/math] to obtain
[math]\displaystyle{ y^{2}\frac{\mathrm{d}^{2}\rho_{n}}{\mathrm{d}y^{2}}+y\frac{\mathrm{d}\rho_{n} }{\rm{d}y}-(n^{2}+y^{2})\rho_{n}=0 }[/math]
The solution of this equation is a linear combination of the modified Bessel functions of order [math]\displaystyle{ n }[/math], [math]\displaystyle{ I_{n}(y) }[/math] and [math]\displaystyle{ K_{n}(y) }[/math] Abramowitz and Stegun 1964. Since the solution must be bounded we know that under the plate the solution will be a linear combination of [math]\displaystyle{ I_{n}(y) }[/math] while outside the plate the solution will be a linear combination of [math]\displaystyle{ K_{n}(y) }[/math]. Therefore the potential can be expanded as
[math]\displaystyle{ \phi(r,\theta,z)=\sum_{n=-\infty}^{\infty}\sum_{m=0}^{\infty}a_{mn}K_{n} (k_{m}r)e^{i n\theta}\phi_{m}(z), \;\;r\gt a }[/math]
and
[math]\displaystyle{ \phi(r,\theta,z)=\sum_{n=-\infty}^{\infty}\sum_{m=-2}^{\infty}b_{mn} I_{n}(\kappa_{m}r)e^{i n\theta}\psi_{m}(z), \;\;r\lt a }[/math]
where [math]\displaystyle{ a_{mn} }[/math] and [math]\displaystyle{ b_{mn} }[/math] are the coefficients of the potential in the open water and the plate covered region respectively.
Incident potential
The incident potential is a wave of amplitude [math]\displaystyle{ A }[/math] in displacement travelling in the positive [math]\displaystyle{ x }[/math]-direction. The incident potential can therefore be written as
[math]\displaystyle{ \phi^{\mathrm{I}} =\frac{A}{i\sqrt{\alpha}}e^{k_{0}x}\phi_{0}\left( z\right) =\sum\limits_{n=-\infty}^{\infty}e_{n}I_{n}(k_{0}r)\phi_{0}\left(z\right) e^{i n \theta} }[/math]
where [math]\displaystyle{ e_{n}=A/\left(i\sqrt{\alpha}\right) }[/math] (we retain the dependence on [math]\displaystyle{ n }[/math] for situations where the incident potential might take another form).
Boundary conditions
The boundary conditions for the plate also have to be considered. The vertical force and bending moment must vanish, which can be written as
[math]\displaystyle{ \left[\bar{\Delta}-\frac{1-\nu}{r}\left(\frac{\partial}{\partial r} +\frac{1}{r}\frac{\partial^{2}}{\partial\theta^{2}}\right)\right] w=0\,\,\,(3) }[/math]
and
[math]\displaystyle{ \left[ \frac{\partial}{\partial r}\bar{\Delta}-\frac{1-\nu}{r^{2}}\left( \frac{\partial}{\partial r}+\frac{1}{r}\right) \frac{\partial^{2}} {\partial\theta^{2}}\right] w=0 \,\,\,(4) }[/math]
where [math]\displaystyle{ w }[/math] is the time-independent surface displacement, [math]\displaystyle{ \nu }[/math] is Poisson's ratio, and [math]\displaystyle{ \bar{\Delta} }[/math] is the polar coordinate Laplacian
[math]\displaystyle{ \bar{\Delta}=\frac{\partial^{2}}{\partial r^{2}}+\frac{1}{r}\frac{\partial }{\partial r}+\frac{1}{r^{2}}\frac{\partial^{2}}{\partial\theta^{2}} }[/math]
Displacement of the plate
The surface displacement and the water velocity potential at the water surface are linked through the kinematic boundary condition
[math]\displaystyle{ \phi_{z}=-i\sqrt{\alpha}w,\,\,\,z=0 }[/math]
From equations (\ref{bvp_plate}) the potential and the surface displacement are therefore related by
[math]\displaystyle{ w=i\sqrt{\alpha}\phi,\quad r\gt a }[/math]
and
[math]\displaystyle{ (\beta\bar{\Delta}^{2}+1-\alpha\gamma)w=i\sqrt{\alpha}\phi,\quad r\lt a }[/math]
The surface displacement can also be expanded in eigenfunctions as
[math]\displaystyle{ w(r,\theta)=\sum_{n=-\infty}^{\infty}\sum_{m=0}^{\infty}i\sqrt{\alpha} a_{mn}K_{n}(k_{m}r)e^{i n\theta},\;\;r\gt a }[/math]
and:
[math]\displaystyle{ w(r,\theta)= \sum_{n=-\infty}^{\infty}\sum_{m=-2}^{\infty}i\sqrt{\alpha}(\beta\kappa _{m}^{4}+1-\alpha\gamma)^{-1}b_{mn}I_{n}(\kappa_{m}r)e^{i n\theta},\; r\lt a }[/math]
using the fact that
[math]\displaystyle{ \bar{\Delta}\left( I_{n}(\kappa_{m}r)e^{i n\theta}\right) =\kappa_{m} ^{2}I_{n}(\kappa_{m}r)e^{i n\theta}\,\,\,(5) }[/math]
An infinite dimensional system of equations
The boundary conditions (3) and (4) can be expressed in terms of the potential using (5). Since the angular modes are uncoupled the conditions apply to each mode, giving
[math]\displaystyle{ \sum_{m=-2}^{\infty}(\beta\kappa_{m}^{4}+1-\alpha\gamma)^{-1}b_{mn} \left(\kappa_{m}^{2}I_{n}(\kappa_{m}a)-\frac{1-\nu}{a}\left(\kappa _{m}I_{n}^{\prime}(\kappa_{m}a)-\frac{n^{2}}{a}I_{n}(\kappa_{m}a)\right) \right) =0\,\,\,(6) }[/math]
[math]\displaystyle{ \sum_{m=-2}^{\infty}(\beta\kappa_{m}^{4}+1-\alpha\gamma)^{-1}b_{mn} \left( \kappa_{m}^{3}I_{n}^{\prime}(\kappa_{m}a)+n^{2}\frac{1-\nu}{a^{2} }\left( \kappa_{m}I_{n}^{\prime}(\kappa_{m}a)+\frac{1}{a}I_{n}(\kappa _{m}a)\right) \right) =0\,\,\,(7) }[/math]
The potential and its derivative must be continuous across the transition from open water to the plate covered region. Therefore, the potentials and their derivatives at [math]\displaystyle{ r=a }[/math] have to be equal. Again we know that this must be true for each angle and we obtain
[math]\displaystyle{ e_{n}I_{n}(k_{0}a)\phi_{0}\left( z\right) + \sum_{m=0}^{\infty} a_{mn} K_{n}(k_{m}a)\phi_{m}\left( z\right) =\sum_{m=-2}^{\infty}b_{mn}I_{n}(\kappa_{m}a)\psi_{m}(z) }[/math]
and
[math]\displaystyle{ e_{n}k_{0}I_{n}^{\prime}(k_{0}a)\phi_{0}\left( z\right) +\sum _{m=0}^{\infty} a_{mn}k_{m}K_{n}^{\prime}(k_{m}a)\phi_{m}\left( z\right) =\sum_{m=-2}^{\infty}b_{mn}\kappa_{m}I_{n}^{\prime}(\kappa_{m}a)\psi _{m}(z) }[/math]
for each [math]\displaystyle{ n }[/math]. We solve these equations by multiplying both equations by [math]\displaystyle{ \phi_{l}(z) }[/math] and integrating from [math]\displaystyle{ -H }[/math] to [math]\displaystyle{ 0 }[/math] to obtain:
[math]\displaystyle{ e_{n}I_{n}(k_{0}a)A_{0}\delta_{0l}+a_{ln}K_{n}(k_{l}a)A_{l} =\sum_{m=-2}^{\infty}b_{mn}I_{n}(\kappa_{m}a)B_{ml} \,\,\,(8) }[/math]
and
[math]\displaystyle{ e_{n}k_{0}I_{n}^{\prime}(k_{0}a)A_{0}\delta_{0l}+a_{ln}k_{l}K_{n}^{\prime }(k_{l}a)A_{l} =\sum_{m=-2}^{\infty}b_{mn}\kappa_{m}I_{n}^{\prime}(\kappa_{m} a)B_{ml} \,\,\,(9) }[/math]
Equation (8) can be solved for the open water coefficients [math]\displaystyle{ a_{mn} }[/math]
[math]\displaystyle{ a_{ln}=-e_{n}\frac{I_{n}(k_{0}a)}{K_{n}(k_{0}a)}\delta_{0l}+\sum _{m=-2}^{\infty}b_{mn}\frac{I_{n}(\kappa_{m}a)B_{ml}}{K_{n}(k_{l}a)A_{l}} }[/math]
which can then be substituted into equation (9) to give us
[math]\displaystyle{ \left( k_{0}I_{n}^{\prime}(k_{0}a)-k_{0}\frac{K_{n}^{\prime}(k_{0} a)}{K_{n}(k_{0}a)}I_{n}(k_{0}a)\right) e_{n}A_{0}\delta_{0l} =\sum_{m=-2}^{\infty}\left( \kappa_{m}I_{n}^{\prime}(\kappa_{m} a)-k_{l}\frac{K_{n}^{\prime}(k_{l}a)}{K_{n}(k_{l}a)}I_{n}(\kappa _{m}a)\right) B_{ml}b_{mn}\,\,\,(10) }[/math]
for each [math]\displaystyle{ n }[/math]. Together with equations (6) and (7) equation (10) gives the required equations to solve for the coefficients of the water velocity potential in the plate covered region.
Numerical Solution
To solve the system of equations (10) together with the boundary conditions (6 and 7) we set the upper limit of [math]\displaystyle{ l }[/math] to be [math]\displaystyle{ M }[/math]. We also set the angular expansion to be from [math]\displaystyle{ n=-N }[/math] to [math]\displaystyle{ N }[/math]. This gives us
[math]\displaystyle{ \phi(r,\theta,z)=\sum_{n=-N}^{N}\sum_{m=0}^{M}a_{mn}K_{n}(k_{m}r)e^{i n\theta }\phi_{m}(z), \;\;r\gt a }[/math]
and
[math]\displaystyle{ \phi(r,\theta,z)=\sum_{n=-N}^{N}\sum_{m=-2}^{M}b_{mn}I_{n}(\kappa _{m}r)e^{i n\theta}\psi_{m}(z), \;\;r\lt a }[/math]
Since [math]\displaystyle{ l }[/math] is an integer with [math]\displaystyle{ 0\leq l\leq M }[/math] this leads to a system of [math]\displaystyle{ M+1 }[/math] equations. The number of unknowns is [math]\displaystyle{ M+3 }[/math] and the two extra equations are obtained from the boundary conditions for the free plate (6) and (7). The equations to be solved for each [math]\displaystyle{ n }[/math] are
[math]\displaystyle{ \left( k_{0}I_{n}^{\prime}(k_{0}a)-k_{0}\frac{K_{n}^{\prime}(k_{0} a)}{K_{n}(k_{0}a)}I_{n}(k_{0}a)\right) e_{n}A_{0}\delta_{0l} =\sum_{m=-2}^{M}\left( \kappa_{m}I_{n}^{\prime}(\kappa_{m}a)-k_{l} \frac{K_{n}^{\prime}(k_{l}a)}{K_{n}(k_{l}a)}I_{n}(\kappa_{m}a)\right) B_{ml}b_{mn} }[/math]
[math]\displaystyle{ \sum_{m=-2}^{M}(\beta\kappa_{m}^{4}+1-\alpha\gamma)^{-1}b_{mn} \left( \kappa_{m}^{2}I_{n}(\kappa_{m}a)-\frac{1-\nu}{a}\left( \kappa _{m}I_{n}^{\prime}(\kappa_{m}a)-\frac{n^{2}}{a}I_{n}(\kappa_{m}a)\right) \right) =0 }[/math]
and
[math]\displaystyle{ \sum_{m=-2}^{M}(\beta\kappa_{m}^{4}+1-\alpha\gamma)^{-1}b_{mn} \left( \kappa_{m}^{3}I_{n}^{\prime}(\kappa_{m}a)+n^{2}\frac{1-\nu}{a^{2} }\left( \kappa_{m}I_{n}^{\prime}(\kappa_{m}a)+\frac{1}{a}I_{n}(\kappa _{m}a)\right) \right) =0 }[/math]
It should be noted that the solutions for positive and negative [math]\displaystyle{ n }[/math] are identical so that they do not both need to be calculated. There are some minor simplifications which are a consequence of this which are discussed in more detail in Zilman and Miloh 2000.
The Shallow Depth Theory of Zilman and Miloh 2000
The shallow water theory of Zilman and Miloh 2000 can be recovered by simply setting the depth shallow enough that the shallow water theory is valid and setting [math]\displaystyle{ M=0 }[/math]. If the shallow water theory is valid then the first three roots of the dispersion equation for the ice will be exactly the same roots found in the shallow water theory by solving the polynomial equation. The system of equations has four unknowns (three under the plate and one in the open water) exactly as for the theory of Zilman and Miloh 2000.
Numerical Results
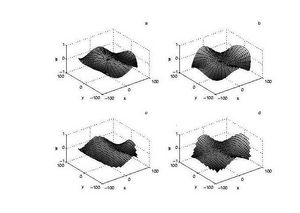
We present solutions for a plate of radius [math]\displaystyle{ a=100 }[/math]. The wavelength is [math]\displaystyle{ \lambda=50 }[/math] (recall that [math]\displaystyle{ \alpha=2\pi/\lambda\tanh\left( 2\pi H/\lambda\right) }[/math]), [math]\displaystyle{ \beta=10^{5} }[/math] and [math]\displaystyle{ \gamma=0 }[/math]. We compare with the method presented in Meylan 2002 for an arbitrary shaped plate modified to compute the solution for finite depth. The circle is represented in this scheme by square panels which are arranged to, as nearly as possible, form a circular shape.
Figure 1 shows the real part (a and c) and imaginary part (b and d) of the displacement for depth [math]\displaystyle{ H=25 }[/math]. The number of points in the angular expansion is [math]\displaystyle{ N=16 }[/math]. The number of roots of the dispersion equation is [math]\displaystyle{ M=8 }[/math]. Plots (a) and (b) are calculated using the circular plate method described here. Plots (c) and (d) are calculated using an arbitrary shaped plate method, with the panels shown being the actual panels used in the calculation. We see the expected agreement between the two methods.
The table below shows the values of the coefficients
[math]\displaystyle{ b_{mn} }[/math] for the case for previous case ([math]\displaystyle{ \lambda=50 }[/math],
[math]\displaystyle{ a=100 }[/math], [math]\displaystyle{ \beta=10^5 }[/math], [math]\displaystyle{ \gamma=0 }[/math], and [math]\displaystyle{ H=25 }[/math]). The very rapid
decay of the higher evanescent modes is apparent. This shows how efficient this method of
solution is since only a small number of modes are required.
[math]\displaystyle{ b_{mn} }[/math] [math]\displaystyle{ n=0 }[/math] [math]\displaystyle{ n=1 }[/math] [math]\displaystyle{ n=2 }[/math] [math]\displaystyle{ n=3 }[/math] [math]\displaystyle{ m=-2 }[/math] [math]\displaystyle{ 1.32 \!\times\!10^{-1}-9.71 \!\times\!10^{-1}i }[/math] [math]\displaystyle{ 6.85 \!\times\!10^{-1} -6.37 \!\times\!10^{-1}i }[/math] [math]\displaystyle{ 2.95 \!\times\!10^{-1}-1.12 \!\times\!10^{0}i }[/math] [math]\displaystyle{ 6.09 \!\times\!10^{-1} -4.95 \!\times\!10^{-1}i }[/math] [math]\displaystyle{ m=-1 }[/math] [math]\displaystyle{ -6.38 \!\times\!10^{-5}+1.47 \!\times\!10^{-3}i }[/math] [math]\displaystyle{ -3.92 \!\times\!10^{-3} + 3.99 \!\times\!10^{-3}i }[/math] [math]\displaystyle{ 1.41 \!\times\!10^{-3}+2.82 \!\times\!10^{-3}i }[/math] [math]\displaystyle{ -4.28 \!\times\!10^{-3} +3.89 \!\times\!10^{-3}i }[/math] [math]\displaystyle{ m=0 }[/math] [math]\displaystyle{ -3.29 \!\times\!10^{-4}+1.43 \!\times\!10^{-3}i }[/math] [math]\displaystyle{ 4.26 \!\times\!10^{-3} -3.62 \!\times\!10^{-3}i }[/math] [math]\displaystyle{ -2.62 \!\times\!10^{-3}+1.76 \!\times\!10^{-3}i }[/math] [math]\displaystyle{ 4.68 \!\times\!10^{-3} -3.39 \!\times\!10^{-3}i }[/math] [math]\displaystyle{ m=1 }[/math] [math]\displaystyle{ 4.31 \!\times\!10^{-7}-3.18 \!\times\!10^{-6}i }[/math] [math]\displaystyle{ -6.64 \!\times\!10^{-6} -7.14 \!\times\!10^{-6}i }[/math] [math]\displaystyle{ 2.07 \!\times\!10^{-7}-7.89 \!\times\!10^{-7}i }[/math] [math]\displaystyle{ -6.30 \!\times\!10^{-6} -7.74 \!\times\!10^{-6}i }[/math] [math]\displaystyle{ m=2 }[/math] [math]\displaystyle{ 6.79 \!\times\!10^{-13}-5.01 \!\times\!10^{-12}i }[/math] [math]\displaystyle{ -5.78 \!\times\!10^{-12}-6.21 \!\times\!10^{-12}i }[/math] [math]\displaystyle{ 8.87 \!\times\!10^{-13}-3.38 \!\times\!10^{-12}i }[/math] [math]\displaystyle{ -5.54 \!\times\!10^{-12}-6.81 \!\times\!10^{-12}i }[/math] [math]\displaystyle{ m=3 }[/math] [math]\displaystyle{ 1.35 \!\times\!10^{-18}-9.95 \!\times\!10^{-18}i }[/math] [math]\displaystyle{ -9.69 \!\times\!10^{-18}-1.04 \!\times\!10^{-17}i }[/math] [math]\displaystyle{ 1.94 \!\times\!10^{-18}-7.39 \!\times\!10^{-18}i }[/math] [math]\displaystyle{ -9.37 \!\times\!10^{-18}-1.15 \!\times\!10^{-17}i }[/math]