Boundary Element Method for the Radiation Potential in Finite Depth

This is an incomplete page

Introduction

We show how to solve for the radiation potential for a rigid body and the surrounding fluid in constant Finite Depth using the Boundary Element Method. The method is a modified version of the Boundary Element Method for a Fixed Body in Finite Depth described previously.

Equations

The linearised frequency-domain equations of motion for a floating body are

[math]\displaystyle{ \Delta\phi=0, \, -h\lt z\lt 0,\,\,\,\mathbf{x} \in \Omega }[/math] [math]\displaystyle{ \partial_n\phi = 0, \, z=-h, }[/math] [math]\displaystyle{ \partial_n \phi = \alpha \phi,\,z=0,\,\,\mathbf{x} \in \partial \Omega_{\mathrm{F}}, }[/math]

(note that the last expression can be obtained from combining the expressions:

[math]\displaystyle{ \partial_n \phi =\mathrm{i} \omega \zeta,\,z=0,\,\,\mathbf{x} \in \partial \Omega_{\mathrm{F}}, }[/math] [math]\displaystyle{ \mathrm{i} \omega \phi = -g\zeta,\,z=0,\,\,\mathbf{x} \in \partial \Omega_{\mathrm{F}}, }[/math]

where [math]\displaystyle{ \alpha = \omega^2/g }[/math]). The body boundary condition for a rigid body is

[math]\displaystyle{ \partial_{n}\phi=Vn_{3},\ \ \mathbf{x}\in\partial\Omega_{\mathrm{B}}, }[/math]

where we assume the body is constrained to move in heave only and [math]\displaystyle{ n_{3} }[/math] is the [math]\displaystyle{ z }[/math]-component of the normal coordinate on the body. The motion of the structure described by the velocity [math]\displaystyle{ V }[/math] is determined from the equation of motion

[math]\displaystyle{ [\rho g W-\omega^2(M+a_{33}(\omega)+ib_{33}(\omega)/\omega) ]V=-i\omega F^{S}(\omega)\,. }[/math]

A wave train incident upon a floating body will be diffracted and will also cause the body to move and so, by linear superposition, the solution will consist of a scattering potential and radiation potential

[math]\displaystyle{ \phi=\phi_{S}+\phi_{R}\,. }[/math]

The scattering potential [math]\displaystyle{ \Phi_{S} }[/math] is just the solution to the problem of a fixed body scattering incident waves and the details of the problem and solution are described in Boundary Element Method for a Fixed Body in Finite Depth. The boundary condition on the structure surface is

[math]\displaystyle{ \partial_{n}\phi_{S}=0,\ \ \mathbf{x}\in\partial\Omega_{\mathrm{B}}, }[/math]

for the scattering problem. The radiation potential [math]\displaystyle{ \Phi_{R} }[/math] is the solution to the radiation problem where a body is forced to oscillate in the absence of incident waves. In this case the body boundary condition is

[math]\displaystyle{ \partial_{n}\phi_{R}=V n_{3},\ \ \mathbf{x}\in\partial\Omega_{\mathrm{B}} }[/math]

and thus the total potential [math]\displaystyle{ \phi }[/math] satisfies the floating body boundary condition. In the case of a body constrained to move in heave it is typical to write the radiation potential as [math]\displaystyle{ \phi_R = V\phi_{3} }[/math] where the velocity [math]\displaystyle{ V }[/math] can be determined from the equation of motion for the floating body. The heave radiation potential thus satisfies Laplace's equation throughout the fluid, the usual sea-bed and free-surface boundary conditions and the body boundary condition

[math]\displaystyle{ \partial_{n}\phi_{3}= n_{3},\ \ \mathbf{x}\in\partial\Omega_{\mathrm{B}}. }[/math]

Hence, [math]\displaystyle{ \phi_{3} }[/math] describes the wave-field due to the heave oscillations of the body with unit amplitude. The radiation potential must also satisfy the radiation condition for outgoing waves which is

[math]\displaystyle{ \left( \frac{\partial}{\partial|x|}-k_0\right) \phi=0,\;\mathrm{{as\;}}|x|\rightarrow\infty\mathrm{.} }[/math]

in two dimensions.

Solution Method

We divide the domain into three regions, [math]\displaystyle{ x\lt -l }[/math], [math]\displaystyle{ x\gt r }[/math], and [math]\displaystyle{ -l\lt x\lt r }[/math] so that the body surface is entirely in the finite region.

Solution in the finite region

We use the Boundary Element Method in the finite region.

Solution in the Semi-infinite Domains

We now solve Laplace's equation in the semi-infinite domains. First consider the domain on the left so that [math]\displaystyle{ \Omega = \left\{ x\lt -l,\;-h\leq z\leq 0\right\} }[/math] The equations are

[math]\displaystyle{ \begin{align} \Delta\phi &=0, &-h\lt z\lt 0,\,\,\mathbf{x} \in \Omega \\ \partial_z\phi &= 0, &z=-h, \\ \partial_z \phi &= \alpha \phi, &z=0,\,\,\mathbf{x} \in \partial \Omega_{\mathrm{F}}, \end{align} }[/math]

(note that the last expression can be obtained from combining the expressions:

[math]\displaystyle{ \begin{align} \partial_z \phi &= -\mathrm{i} \omega \zeta, &z=0,\,\,\mathbf{x} \in \partial \Omega_{\mathrm{F}}, \\ \mathrm{i} \omega \phi &= g\zeta, &z=0,\,\,\mathbf{x} \in \partial \Omega_{\mathrm{F}}, \end{align} }[/math]

where [math]\displaystyle{ \alpha = \omega^2/g \, }[/math]) We have the following explicit boundary conditions

[math]\displaystyle{ \phi =f\left( z\right) ,\;\;x=-\,l }[/math]

and

[math]\displaystyle{ \lim\limits_{x\rightarrow -\infty }\phi \left( x,z\right) = R\phi_0 e^{k_{0}x}, }[/math]

(this must hold to satisfy the radiation condition) where [math]\displaystyle{ f\left( z\right) }[/math] is an arbitrary continuous function[math]\displaystyle{ . }[/math] Our aim is to find the outward normal derivative of the potential on [math]\displaystyle{ x=-l }[/math] as a function of [math]\displaystyle{ \tilde{\phi}\left( z\right) }[/math]. [math]\displaystyle{ \phi_0 }[/math] and [math]\displaystyle{ k_0 }[/math] will be defined shortly when we separate variables, but are equivalent to the Sommerfeld Radiation Condition.

Since the water depth is constant in these regions we can solve Laplace's equation by separation of variables.

Separation of variables for a free surface

We use separation of variables

We express the potential as

[math]\displaystyle{ \phi(x,z) = X(x)Z(z)\, }[/math]

and then Laplace's equation becomes

[math]\displaystyle{ \frac{X^{\prime\prime}}{X} = - \frac{Z^{\prime\prime}}{Z} = k^2 }[/math]

The separation of variables equation for deriving free surface eigenfunctions is as follows:

[math]\displaystyle{ Z^{\prime\prime} + k^2 Z =0. }[/math]

subject to the boundary conditions

[math]\displaystyle{ Z^{\prime}(-h) = 0 }[/math]

and

[math]\displaystyle{ Z^{\prime}(0) = \alpha Z(0) }[/math]

We can then use the boundary condition at [math]\displaystyle{ z=-h \, }[/math] to write

[math]\displaystyle{ Z = \frac{\cos k(z+h)}{\cos kh} }[/math]

where we have chosen the value of the coefficent so we have unit value at [math]\displaystyle{ z=0 }[/math]. The boundary condition at the free surface ([math]\displaystyle{ z=0 \, }[/math]) gives rise to:

[math]\displaystyle{ k\tan\left( kh\right) =-\alpha \, }[/math]

which is the Dispersion Relation for a Free Surface

The above equation is a transcendental equation. If we solve for all roots in the complex plane we find that the first root is a pair of imaginary roots. We denote the imaginary solutions of this equation by [math]\displaystyle{ k_{0}=\pm ik \, }[/math] and the positive real solutions by [math]\displaystyle{ k_{m} \, }[/math], [math]\displaystyle{ m\geq1 }[/math]. The [math]\displaystyle{ k \, }[/math] of the imaginary solution is the wavenumber. We put the imaginary roots back into the equation above and use the hyperbolic relations

[math]\displaystyle{ \cos ix = \cosh x, \quad \sin ix = i\sinh x, }[/math]

to arrive at the dispersion relation

[math]\displaystyle{ \alpha = k\tanh kh. }[/math]

We note that for a specified frequency [math]\displaystyle{ \omega \, }[/math] the equation determines the wavenumber [math]\displaystyle{ k \, }[/math].

Finally we define the function [math]\displaystyle{ Z(z) \, }[/math] as

[math]\displaystyle{ \chi_{m}\left( z\right) =\frac{\cos k_{m}(z+h)}{\cos k_{m}h},\quad m\geq0 }[/math]

as the vertical eigenfunction of the potential in the open water region. From Sturm-Liouville theory the vertical eigenfunctions are orthogonal. They can be normalised to be orthonormal, but this has no advantages for a numerical implementation. It can be shown that

[math]\displaystyle{ \int\nolimits_{-h}^{0}\chi_{m}(z)\chi_{n}(z) \mathrm{d} z=A_{n}\delta_{mn} }[/math]

where

[math]\displaystyle{ A_{n}=\frac{1}{2}\left( \frac{\cos k_{n}h\sin k_{n}h+k_{n}h}{k_{n}\cos ^{2}k_{n}h}\right). }[/math]

Expansion of the potential

This gives us the following expression for the potential in the region [math]\displaystyle{ \Omega }[/math]

[math]\displaystyle{ \phi \left( x,z\right) = \sum_{m=0}^{\infty } a_m \phi _{m}\left( z\right) e^{k_{m}\left( x+l\right) } }[/math]

where [math]\displaystyle{ a_m }[/math] can be found from [math]\displaystyle{ \left. \phi \right| _{x=-l} = f(z) }[/math] from the orthogonality of the vertical eigenfunctions. Therefore

[math]\displaystyle{ a_m = \frac{1}{A_m} \int_{-h}^{0} f(z) \phi_m(z) \mathrm{d}z }[/math]

The normal derivative of potential (with the normal outward from the interior region) we obtain

[math]\displaystyle{ \partial_n\left. \phi \right| _{x=-l} = -\partial_x \left. \phi \right| _{x=-l} =- \sum_{m=0}^{\infty } k_m a_m \phi _{m}\left( z\right) }[/math]

If we define [math]\displaystyle{ \mathbf{Q} }[/math] as

[math]\displaystyle{ \mathbf{Q} \left[f\left( z\right) \right]= -\sum_{m=0}^{\infty } \frac{k_{m}}{A_m} \left\{ \int_{-h}^{0} f\left( s\right) \phi _{m}\left( s\right) \mathrm{d}s \right\} \phi _{m}\left( z\right) }[/math]

we can write

[math]\displaystyle{ \partial_n \left. \phi \right| _{x=-l} =\mathbf{Q} \left[ f(z) \right], }[/math]

Similarly, we now consider the potential in the region [math]\displaystyle{ \Omega = \left\{ x\gt r,\;-h\leq z\leq 0\right\} }[/math] which satisfies exactly the equations as before except the boundary condition is

[math]\displaystyle{ \lim\limits_{x\rightarrow \infty }\phi \left( x,z\right) = \phi_0 T e^{-k_{0}x} }[/math]

We solve again by separation of variables and obtain

[math]\displaystyle{ \left. \partial_n \phi \right| _{x=r}= \left. \partial_x \phi \right| _{x=r}=\mathbf{Q}\left[f\left( z\right)\right] , }[/math]

where the outward normal is with respect to the inner domain as before. Note that, if the depth is different on each side then the matrix [math]\displaystyle{ \mathbf{Q} }[/math] will be different (since we need to use a different depth solving the Dispersion Relation for a Free Surface etc.)

Boundary Element Method

We have reduced the problem to Laplace's equation in a finite domain subject to certain boundary conditions. These boundary conditions give the outward normal derivative of the potential as a function of the potential but this is not always a point-wise condition; on some boundaries it is given by an integral equation. We must solve both Laplace's equation and the integral equations numerically. We will solve Laplace's equation by the Boundary Element Method and the integral equations by numerical integration. However, the same discretisation of the boundary will be used for both numerical solutions. We solve Laplace's equation by a modified constant panel method which reduces it to the following matrix equation

[math]\displaystyle{ \frac{1}{2}\vec{\phi}=\partial_n\mathbf{G}\vec{\phi}-\mathbf{G}\partial_n\vec{\phi}. }[/math]

where [math]\displaystyle{ \vec{\phi}\mathcal{\ } }[/math]and [math]\displaystyle{ \partial_n\vec{\phi} }[/math] are vectors which approximate the potential and its normal derivative around the boundary [math]\displaystyle{ \partial \Omega }[/math], and [math]\displaystyle{ \mathbf{G} }[/math] and [math]\displaystyle{ \mathbf{G}_{n} }[/math] are matrices corresponding to the Green function and the outward normal derivative of the Green function respectively. The method used to calculate the elements of the matrices [math]\displaystyle{ \mathbf{G} }[/math] and [math]\displaystyle{ \partial_n\mathbf{G} }[/math] can be found in Boundary Element Method.

The outward normal derivative of the potential, [math]\displaystyle{ \partial_n\vec{\phi}, }[/math] and the potential, [math]\displaystyle{ \vec{\phi}, }[/math] are related by the conditions on the boundary [math]\displaystyle{ \partial \Omega }[/math]. This can be expressed as

[math]\displaystyle{ \partial_n\vec{\phi}=\mathbf{A}\,\vec{\phi}-\vec{f}, }[/math]

where [math]\displaystyle{ \mathbf{A} }[/math] is the block diagonal matrix given by

[math]\displaystyle{ \mathbf{A}\mathbb{=}\left[ \begin{matrix} \mathbf{Q} & & & & \\ & \mathbf{Q} & & \\ & & \alpha \,\mathbf{I} & \\ & & & 0 & \\ & & & & 0 \end{matrix} \right] , }[/math]

where we have separated the boundaries to the semi-infinite domains, the free surface and the body boundary and the sea floor. [math]\displaystyle{ \mathbf{Q} }[/math] is a matrix approximation of the integral operator of the same name and [math]\displaystyle{ \vec{f} }[/math] is the vector

[math]\displaystyle{ \vec{f}=\left[ \begin{matrix} 0 \\ 0 \\ 0 \\ 0 \\ n_{3} \end{matrix} \right] }[/math]

which specifies the body boundary condition for the radiation problem.

We obtain the following matrix equation for the potential

[math]\displaystyle{ \left( \frac{1}{2}\ \mathbf{I}-\mathbf{G}_{n}+\mathbf{GA}\right) \vec{\phi}=\mathbf{G} \vec{f} }[/math]

which can be solved straightforwardly. The reflection and transmission coefficients are calculated from the solution.

Numerical Calculation of [math]\displaystyle{ \mathbf{Q} }[/math]

We begin by truncating to a finite number ([math]\displaystyle{ N }[/math]) of evanescent modes,

[math]\displaystyle{ \mathbf{Q}\left[ f \right] =-\sum_{m=0}^{N}k_{m}\int_{-h}^{0} f\left( s\right) \phi_{m}\left( s\right) \mathrm{d}s \frac{\phi _{m} \left( z\right)}{A_m} . }[/math]

We calculate the integral with the same panels as we used to approximate the integrals of the Green function and its normal derivative . Similarly, we assume that [math]\displaystyle{ f(s) \, }[/math] is constant over each panel and integrate [math]\displaystyle{ \phi _{m}\left( s\right) }[/math] exactly. This gives us the following matrix factorisation of [math]\displaystyle{ \mathbf{Q} }[/math]

[math]\displaystyle{ \mathbf{Q}[f]=\mathbf{S}\,\mathbf{R}\,[f]. }[/math]

The components of the matrices [math]\displaystyle{ \mathbf{S} }[/math] and [math]\displaystyle{ \mathbf{R} }[/math] are

[math]\displaystyle{ s_{jm} = -k_m\phi _{m}\left( z_{j}\right) , }[/math] [math]\displaystyle{ r_{mj} = \frac{1}{A_m} \int_{z_{j}-\Delta x/2}^{z_{j}+\Delta x/2}\phi _{m}\left( s\right) \mathrm{d}s }[/math]

Calculation of the body velocity [math]\displaystyle{ V }[/math]

In order to determine the body velocity it is necessary to use the equation of motion given earlier. However, each of the terms in this equation should be accounted for first. For motion in heave only, the time-dependent equation of motion is

[math]\displaystyle{ M\partial_{t}^2\xi=-\rho\int_{\partial\Omega}\partial_{t}\Phi n_{3} \, dS-\rho g W \xi }[/math]

where [math]\displaystyle{ \xi }[/math] is the displacement of the body. The frequency domain assumption of harmonic motions gives

[math]\displaystyle{ \Phi(\mathbf{x},t)= \textrm{Re} \{ \, \phi(\mathbf{x},t) e^{-i\omega t} \,\}, \quad \xi(t)=\textrm{Re} \{ X e^{-i\omega t} \} }[/math]

where the complex displacement and velocity amplitudes are related by [math]\displaystyle{ X=V/(-i\omega) }[/math]. By substituting these expressions into the equation of motion and decomposing the total frequency-domain potential as described previously, i.e.

[math]\displaystyle{ \phi=\phi_{S}+V\phi_{3}\, }[/math]

we obtain

[math]\displaystyle{ -i\omega M V=i\rho\omega\int_{\partial\Omega} (\phi_{S}+V\phi_{3}) n_{3} \, dS-\rho g W V/(-i\omega) }[/math] [math]\displaystyle{ (\rho gW -\omega^{2}M - \omega^{2}\rho\int_{\partial\Omega}\phi_{3} n_{3}dS)V = -i\omega F^{S} }[/math]

where the last term is the exciting force due to the scattering potential defined by

[math]\displaystyle{ F_{3}^{S}=i\omega\rho\int_{\partial\Omega}\phi_{S}n_{3}dS. }[/math]

The radiation force due to the unit amplitude motion of the body is usually decomposed as follows

[math]\displaystyle{ i\omega\rho\int_{\partial\Omega}\phi_{3}n_{3}dS=i\omega(a_{33}+ib_{33}/\omega) }[/math]

where [math]\displaystyle{ a_{33} }[/math] and [math]\displaystyle{ b_{33} }[/math] are the added mass and damping coefficients. Thus, we arrive at the equation of motion

[math]\displaystyle{ (\rho gW -\omega^{2}M - \omega^{2}(a_{33}+ib_{33}/\omega))V = -i\omega F^{S}.\, }[/math]

Therefore, provided we can calculate the radiation and exciting forces by integration of the potential over the wetted surface the complex velocity amplitude can be computed.

Matlab Code

Plot of the panels used to calculate the solution. Red shows the vertical boundaries, blue the surfaces with vanishing normal derivative and green the free surface.

Curve of [math]\displaystyle{ R }[/math] and [math]\displaystyle{ T }[/math] for the geometry shown in the previous figure

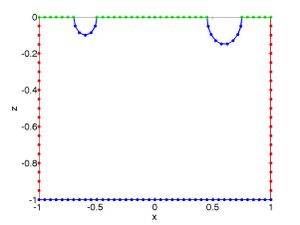
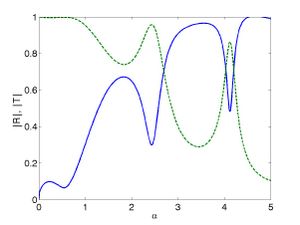
• A program to solve for a fixed body fixed_body_twod.m
• a program to plot the panels can be found here domainplot.m
• a program to generate the panels for two circles can be found here semicircles_two.m
• a program to calculate the solution for a specific geometry (with two plots as output as shown) can be found here wave_bem_example.m

Additional code

This program requires

• dispersion_free_surface.m
• A program to calculate the matrices [math]\displaystyle{ G }[/math] and [math]\displaystyle{ G_{n} }[/math] bem_constant_panel.m